Brain Image Classification - CNN

Date Published: (아직 어떻게 하는지 모른다)

원문 링크

https://www.xuningyang.com/blog/2021-01-11-katex-with-jekyll/ Jekyll 에 Katex 를 적용해 보았다! 앞으로 velog 에서 실컷 쓰고 복붙해도 수식이 그대로 남을 것이다 ㅎㅎ. 다만 ##

Paper 1

Predicting Alzheimer’s disease: a neuroimaging study with 3D convolutional neural networks (2015 Arxiv.)

선정 이유: 높은 citation, 초기 paper, reconstruction idea

인용수가 많아 고르게 되었지만 출판은 되지 않은 paper. 이유는 모르겠다.

MRI 영상에 3D conv. 연산을 사용해서 HC / AD / MCI 분류기를 만들었다고 한다. 각각 755 cases 가 있으며, 모두 SPM 을 사용해 68 x 95 x 79 인 template 로 normalize했음. 추가적으로 평균과 표준편차를 이용해 normalize.

모델은 two-stage 인데, sparse autoencoder 을 사용해 합성곱 필터를 학습힌 뒤, 이를 활용해 classifier 을 만들었음.

Sparse Autoencoder

\[h=f(Wx+b)\newline \hat{x}=g(W^*h+b^*)\]

$x,\hat{x}\in R^n, h\in R^p$ 이라고 하자. Encoder 함수 $f:x \rightarrow h$ 는 input 을 hidden representation 으로 변환하며, decoder 함수 $g:h \rightarrow \hat{x}$ 는 hidden representation 으로 input을 reconstruct 한다.

저자들은 encoder 함수로 sigmoid 를 사용했으며, decoder 함수로는 identity mapping 을 활용했다. Sigmoid 함수는 미분이 가능하며 (-1, 1) 에서 bijective 이기 때문에 변환 함수로 적합하지만 (검증 필요), decoder 에서는 원본의 intensity 로 복원해야 하기 때문에 identity mapping 을 사용해야 한다.

특이한 점은 tied weights (즉, $W^T=W^*$) 을 활용한 것인데, 이는 적은 parameter 을 통해 과적합을 방지하기 위함으로 보인다. (inverse 가 아니라 transpose 를 쓰는 이유는 연산량을 줄이기 위한 heuristic 접근법이 아닌가 싶다).

전체 loss function 은 다음과 같이 정의된다:

\[J(W,b)=\frac{1}{N}\sum_{i=1}^{N}\frac{1}{2}\|\hat{x}^{(i)}-x^{(i)}\|^2 +\beta\sum_{j=1}^hKL(s\|\hat{s}_j) +\lambda\sum_{i,j}W_{i,j}^2\]

첫번째 항은 N개의 sample 에 대한 MSE Loss 를 계산한 것이다. 저자들은 overcomplete (input units 보다 많은) hidden layer 을 사용해서 특징을 추출하려 하는데, 단순한 MSE Loss 를 사용하면 hidden layer 이 identity function 만을 학습할 수 있기 때문에 두번째 항, 즉 sparsity constraint 를 추가했다고 한다. 마지막 항은 과적합을 방지하기 위한 weight decay 이다.

Sparsity constraint

$a_j(x)$를 hidden unit $j$ 의 활성화 함수라고 하자. 이 때, $\hat{s_j}$는 모든 training set N 에 대한 활성화값의 평균이다.

\[\hat{s_j}=\frac{1}{N}\sum_{i=1}^N[a_j(x^{(i)})]\]

저자들은 이 값을 $\hat{s_j}=s=0.05$ 같이 0에 가까운 값으로 고정하려고 한다. 즉, 모든 hidden unit 의 activation 값을 평준화 시켜서 데이터에 편향되지 않게 하려는 듯 하다. $\hat{s_j}$ 를 $s$ 에 가깝게 하기 위해서는 단순히 $s$ 와 $\hat{s_j}$ 의 분포를 베르누이로 설정한 뒤 KL Divergence 를 최소화 시키면 된다.

\[\sum_{j=1}^hKL(s\|\hat{s}_j)=slog(\frac{s}{\hat{s_j}})+(1-s)log(\frac{1-s}{1-\hat{s_j}})\]

예를 들어 $s$가 0.05고 $\hat{s_j}$ 가 1에 근접한 값이면, 위 수식은

\[0.05\log(\frac{0.05}{1})+(1-0.05)\log(\frac{1-0.05}{1-1}) \approx \infty\]

…펑 터지겠다. 즉, $\hat{s_j}$ 가 0.05 일 때 KL Divergence 를 최소화 할 수 있겠다.

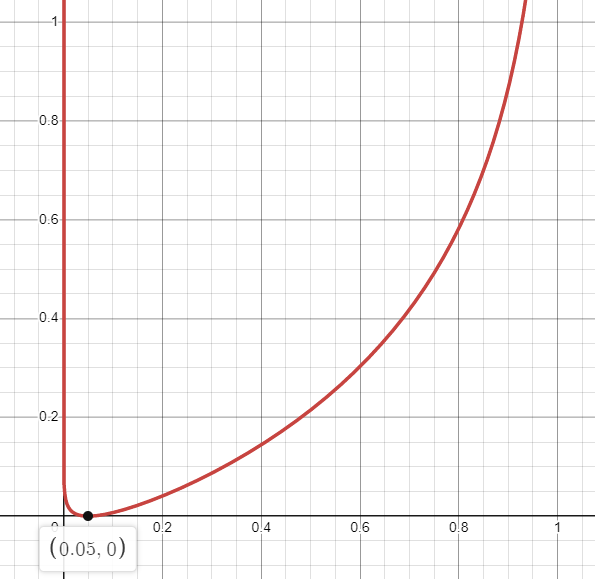
Pretraining scheme

100장의 스캔에서 1000개의 5x5x5 패치를 무작위로 추출. 각 패치를 길이가 125인 벡터로 flatten 한 뒤 미니배치 하강경사법을 사용해 훈련.

3D Convolution

CNN 에서는 hidden unit 이 이전 layer 의 모든 unit 과 연결되어있지 않으며, 이는 parameter 을 줄이는 동시에 local discriminative feature 학습에 유리함. 여기서, 그 hidden unit 이 연결되어 있는 이미지의 부분을 receptive field 라고 하며, 모든 hidden units 를 통틀어 feature map 이라고 칭함. 하나의 hidden layer 내에는 여러개의 feature map이 존재하며, 각 feature map 안에서는 동일한 parameter 이 사용됨.

Architecture 을 살펴보자. 2015년 논문이라서 그런지 현대의 CNN 구조와는 너무나도 다른게 느껴진다. 우선 방금 pretrain 한 망을 사용해서 150 개의 feature map을 생성한 뒤, max pooling 을 한 뒤 flatten 한다. 이 때 결과물은 150x12x18x15 = 486,000 의 길이를 가진다. 이 벡터를 hidden FC layer 을 거쳐 3개의 class 로 분류한다.

저자들은 단순히 cross entropy loss 를 활용했다고 했으며, 여기서는 weight decay 를 사용하지 않았다고 한다.

결과

3-way 는 89.47% 가 나왔다.

모델의 시각화 자료로 합성곱 연산 예시를 보여주었다.

Paper 2

3D convolutional neural networks-based multiclass classification of Alzheimer’s and Parkinson’s diseases using PET and SPECT neuroimaging modalities (2021 Brain informatics)

선정 사유: 공학적인 요소를 참고할 수 있음

Filter 을 11로 고정한 것이 특징. L2 Factor을 사용하고 FC layer을 3개를 쌓았다. 참고할만할듯?

Paper 3

Visual Explanations From Deep 3D Convolutional Neural Networks for Alzheimer’s Disease Classification (2018 AMIA)

선정 사유: Sensitivity Analysis 와 Grad-CAM 활용 사례

Grad-CAM

VGG를 사용했기 때문에 마지막 층이 3x3x3 밖에 안되는 문제가 있다. 따라서, 이전 층에서 Grad CAM 을 적용했다. 개인적으로 low level feature은 reliable 하지 않은 것 같다.

Paper 4

Visualizing Convolutional Networks for MRI-based Diagnosis of Alzheimer’s Disease (MICCAI 2018)

선정 사유: First AD Visualization

Architecture 은 3x3x3 을 8/16/32/64, 그리고 FC 는 128/64 두개. Skull removal 후 standard normalization.

네가지 visualization technique 를 활용한다

• Sensitivity analysis
• Guided backpropagation
• Occlusion / brain area occlusion

Occlusion 방법은 이미지의 일부를 가린 뒤 output의 변화를 관찰한다. 변화가 심할 수록 relevance 가 높은 region 이라는 뜻이다. Brain area occlusion 은 AAL 을 활용해서 brain region 을 가린다. AD의 결과물을 보자.

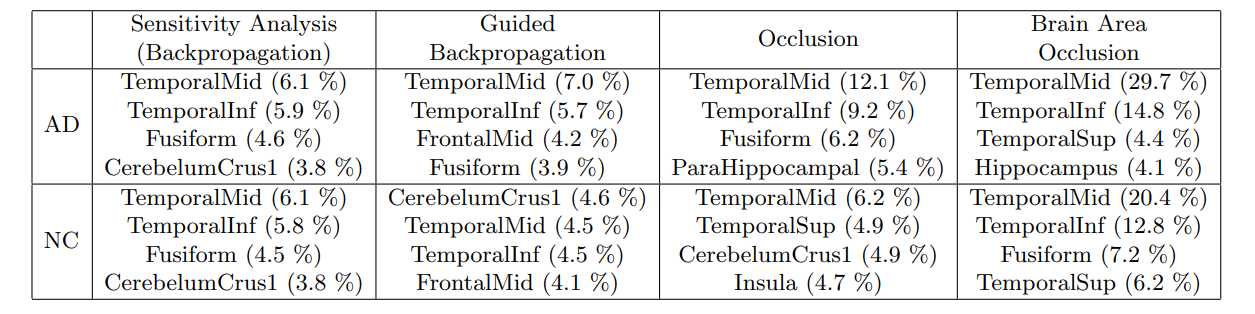
저자는 각 방법을 활용해서 모든 환자의 region 별 importance 를 계산한 뒤 평균을 내렸다. 위 표는 임상적으로 AD 는 medial temporal lobe 가 중요하다는 사실과 결론이 일치하다는 것을 보여준다.

다만, 이 히트맵은 평균임을 주목할 필요가 있다. 저자는 환자사이의 편차가 심하다는 것을 언급했다.

---

Skipped lists

1. Design of A Convolutional Neural Network System to Increase Diagnostic Efficiency of Alzheimer’s Disease (IOP 2019)
2. RESIDUAL AND PLAIN CONVOLUTIONAL NEURAL NETWORKS FOR 3D BRAIN MRI CLASSIFICATION

단순히 ResNet 활용한 논문임. Plain CNN 과 크게 다르지 않다는 점만 note 하면 될듯.

1. Classifcation and Visualization of Alzheimer’s Disease using Volumetric Convolutional Neural Network and Transfer Learning (2019 Nature)

Saliency map 활용함. 채널은 10을 쓰지만, inception layer 은 40. End to end pMCI visualization 을 했다는 게 novelty라고 주장.

Skull stripping 과 segmentation 을 일절 활용하지 않았다는 점은 주목할만 한듯.